Category Archives: Engineering

Trolley Problem Memes

August 14, 2016Economics, Engineering, Idle Speculation, Internet Culture, Machine Learning, Organizing Systems, Thoughts on Thoughtsadmin

Trigger warning: Conversation and possibly dark humour about fictional (and possibly not-so-fictional) people dying in car and train accidents.

How do you design a self-driving car to appropriately value human life? Can you use a Facebook group to speed the development of philosophical discourse?

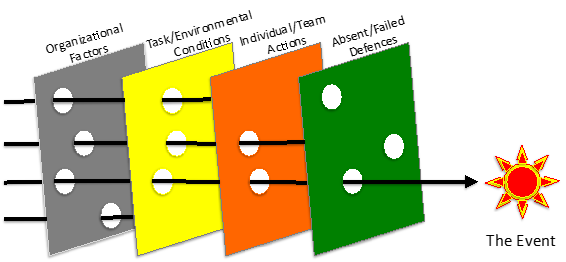
The ‘Trolley Problem‘ is a problem in ethics, first known to be described in its modern form in the early 1950s. Basically, it boils down to the question:

If you have a choice between action and inaction, where both will cause harm, but your action will harm fewer people, is it moral to perform that action?

Interestingly, people answer this question differently, based on how active the action of harm is, the ratio of people hurt between the choices of action and inaction, and other reasons.

The astute will notice that this type of decision problem is a very common one, the most obvious being in military applications, but also vaccines (and invasive health procedures in general), firebreaks, and perhaps the canonical example, automobile design and manufacturing.

This type of decision making has become even more important with the advent of self-driving cars:

Would you drive a car that would choose to drive you into a brick wall rather than run over five pedestrians?

Overall, you would think that this would reduce your risk of fatality, but few people would choose that car, likely because it is a classic prisoner’s dilemma[1][2].

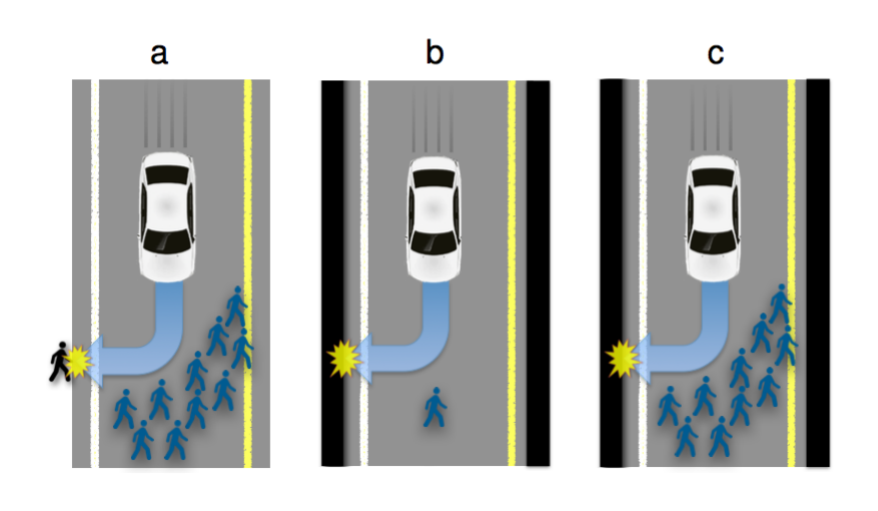
What is your self-driving car's ethical system? — What is your self-driving car’s ethical system?

Personally, I think that much of this conversation is sophistry[3]. If one is truly interested in preserving life, the solution is not to convince self-driving cars to kill different people, but perhaps to have more stringent driving training requirements, to invest in fixing known problem intersections, to invest in better public transit.

So, if these conversations are not useful for anything else, they must be useful in and of themselves, and therefore must be Philosophy[4]!

One of the places that these conversations are occurring is the ‘Trolley Problems Memes Facebook page‘[5].

Now, you can argue that this page is purely for entertainment, but I think there’s a lot more hidden there. There is a fomenting and interchange of ideas, much faster and more fluidly than at any time in history. The person who writes the next book[6] on the ethics of decision making could well be influenced by or be an avid user of a site such as this one.

They may have started with Rick-rolling, but image macros are helping the advancement of human knowledge. Stew on that one for a while.

And while you’re thinking about that, something which ties it all together[7]:

"The creator might argue that his robot is an 'individual', capable of his own decisions, while the opposition would say that he (the creator) is responsible for the algorithm that led to the action. Imagine this happening - it would give birth to one of the greatest on-court debates ever." From Patrice Leiteritz via Trolley Problem Memes — “The creator might argue that his robot is an ‘individual’, capable of his own decisions, while the opposition would say that he (the creator) is responsible for the algorithm that led to the action. Imagine this happening – it would give birth to one of the greatest on-court debates ever.” From Patrice Leiteritz via Trolley Problem Memes

[1]If everyone cooperates, overall they will receive a better result, but if any one of them betrays the others, they get an even better result, but everyone else’s result is much worse. This theoretically leads everyone to betray everyone else, leading to everyone having a worse overall outcome.

[2]People also like the feeling of control.

[3]Check out the article. Apparently, the Sophists were the first (recorded) right-wing think tanks.

[4]My undergrad Philosophy 101 prof. made the argument that because philosophy was not useful for anything else, it must be inherently be useful (and that that was better).

[5]Dark humour. You have been warned.

[6]And it might not even be a book! A blog post, even! 😀

[7]Not a deliberate pun.

How do You Think Before You Speak?

May 23, 2016Engineering, Idle Speculation, Internet Culture, Politics, Puns, Teaching, Thoughts on Thoughtsadmin

I’ve talked a lot about the speed involved and possibly required for retorts and humour, but not all conversation is retorts and counter-retorts[1].

For example, you’re giving a speech or lesson, and someone asks you a question. Many of the same tactics are helpful. It’s helpful to know your audience, to have an idea of their background(s), which types of words will work best for explaining things, and to have an idea of what they perceive the relative level of hierarchy is between you and them.

But once you have an idea of these things, what do you do?

This trigger for this post was an article reporting on Jon Stewart talking about how Hillary Clinton pauses for a few seconds between a question and when she answers[2]:

”
…“It’s — look, there are politicians who are either rendering their inauthenticity in real enough time to appear authentic, and then their are politicians who render their inauthenticity through — it’s like, when your computer … if you have a Mac and you want to play a Microsoft game on it …”

AXELROD: Yes, yes.

STEWART: … and there’s that weird lag.

AXELROD: Yes. No, I mean …

STEWART: That’s Hillary Clinton.

AXELROD: … that’s a big problem. There’s like a seven-second delay and all the words come out in a perfectly …

STEWART: Right.

AXELROD: … politically calibrated sentence.

STEWART: Right. Now, what gives me hope in that is that there’s a delay, which means she’s somehow fighting something. I’ve seen politicians who don’t have that delay and render their inauthenticity in real time, and that’s when you go, ‘That’s a sociopath.’
”

So, when you’re answering a difficult question, do you pause? Why? For how long?

For me, it depends on the type of question. For emotionally difficult questions, some of it is finding a neutral[3] perspective from which to address the question, to speak to the person(s) asking the question in a positive and useful way. Sometimes it’s choosing the appropriate emotional outlet[4] for whatever I’m feeling at the time.

For technically difficult questions, it feels much more like assembling a mental model in my head, or choosing between different visualizations/places to start. Parts of this can feel similar to emotionally difficult questions (perspectives vs. visualizations), but to me they feel quite different[5].

So, how does this work for you?

[1]No matter how much bash.org would want you to think so. (Note that outside that page, bash.org is quite unfiltered internet. You have been warned.)

[2] Article is here. In a footnote because the editorializing in the article is outside the scope of this post.

[3]In the emotional perspective sense.

[4]This is often laughter for later when I’m alone. I mean, really, we’re just ape-like creatures who don’t know the first thing about ourselves. Why are we getting all angry about minutiae? This can only be funny.

[5]Now that I say this, I’ll have to watch next time. But something getting my back[6] up really feels different from trying to focus and assemble a visualization. Maybe being able to relax for all types of questions would make them more similar.

[6]Back hackles?

Slide Rule Accuracy and F=ma

May 19, 2016Engineering, Nostalgia, Teachingadmin

Earlier this week, we were talking about drawing a Large diagram as one of the lasting and important things I learned in Prof. Collins’ Structure & Materials course.

Here are some of the others:

‘Slide Rule Accuracy’

This is the idea that in the real world[1], you’re never going to use more than three digits of accuracy (or four if your number starts with a ‘1’)[2]. Beyond that, things will get lost in the noise, or other inaccuracies, whether it’s budget contingencies, manufacturing defects, or whatever. (It would be interesting to see whether this has changed for manufactured parts with increased automation.)

The ‘3 laws of engineering'[3]:

1) F=ma

Simple, yet profound. When you’re dealing with non-relativistic systems (pretty much all of them), you push on something, it will move or react proportionally. This is not limited to physical systems.

2) You can’t push on a rope.

Also simple, has a number of applications for mechanical systems, but is probably the most ‘Engineer-y’ useful statement for dealing with other people.

3) In order to solve an engineering problem, you must first know the solution.

This one doesn’t really make sense on first blush, but I’ve experienced it. I mentioned earlier that the brain is often a structure that problems flow through, and in a sense this is a statement of that. You’re going to try to fit a new problem you’re looking at into the structure(s) of all the problems that you’ve seen before, and you have a huge advantage if you’ve seen similar problems before, or seen other problems you can apply by analogy.

We also had a ‘notebook’ that we put all of our class notes in, including cut and pasting from technical sheets, and this ‘notebook’ was our open book for the exam. It was a great exercise in focusing note-taking and coalescing your thoughts onto a medium-small piece of paper.

“When someone is paying you $100 for an hour of work, it’s worth paying a few extra cents for a good sheet of paper to give it to them on.”

The course had special ‘engineering notepaper’ that they wanted us to hand problem sets in on. There wasn’t any penalty for not doing so, but the lesson was that a little bit of professional presentation went a long way.

[1]This is when you’re dealing with things of reasonable size. I’m guessing when you’re looking at gravity waves or Higgs bosons, you might be using somewhat more accuracy. But at the same time, you’re probably not really looking at more than the last few digits…

[2]This is one of those subtle things which is actually quite important and powerful. On a slide rule, the portion which starts with a ‘1’ is fully 30% of the length (log10(2) ~=0.301), so unless you use the fourth digit here, you’re losing a substantial portion of your accuracy. There is a better explanation of this here:

[3]For a slightly different set of three Engineering laws, look here:

Draw a LARGE Diagram

May 17, 2016Engineering, Nostalgia, Organizing Systems, Teaching, Thoughts on Thoughts, Visualizationsadmin

Draw a LARGE diagram. When you start, you have no idea which part you’ll be focusing on, so draw it large to start.

In undergrad, we had a Structures and Materials course with Prof. Collins. I owe a lot to that class. It was first year, first term, and it was our first experience with ‘real Engineering’ (with a capital ‘E’).

Collins talked about (along with how to build bridges and other structures) a number of things which you would actually use every day, no matter what types of things you were designing or calculating or planning.

The biggest[1] one is indubitably ‘draw a Large diagram’. Every time I do this, whether it’s on a whiteboard at work, or in my journal[2] at home, it helps far more often than I expect, especially when you’re drawing a teaching diagram, and people are asking questions.

It helps when you’re drawing a semicircle intersected by many lines, with some angles known, some angles not known, and you need to do a bunch of fancy figuring to get the answer[3].

Next time, we’ll talk about some other useful tidbits I learned in that class. Stay tuned!

[1]Ha!

[2]I use notebooks with blank pages. It helps me draw diagrams without extraneous lines, feels freer for thinking.

[3]I think this was a GRE question.

Which ‘Magic Numbers’ do You Use?

May 8, 2016Engineering, Nostalgia, Science!, Thoughts on Thoughts, Words!admin

I was talking with S earlier this week, and the idea came up for a post about the numbers that I remember and use for estimation. I enjoy the sobriquet ‘Magic Numbers’.

‘Magic Numbers’. They’re considered bad practice[1] in programming, but are such a useful and helpful part of human ‘back of the envelope‘ problem solving[2].

Water:

The ‘Magic Number’ which precipitated this post was the fact that one tonne[3] of water is one cubic meter in volume. Interestingly, this is actually a number of interlocking ‘Magic Numbers’, including: One tonne is one thousand kilograms, water has a density of 1 gram per cubic centimetre (‘density of 1’), one thousand is 10x10x10, one tonne is one thousand liters of water, one liter is one kilogram, etc, etc…

I mostly enjoy using this to respond to ‘I could eat a tonne of this’, or to estimate whether you could fit a tankerfull of oil in an office.

It is commonly known that ice will float on water, because the hydrogen bonds give the water molecules a structure which is more spaced out and less dense than close packed[4]. Also, water has its greatest density of about one at about 4 degrees C.

Density:

Incidentally, hydrocarbons have a density of about 0.7, so the tankerful of oil mentioned above would rather difficult to swim in. This 0.7 is close enough to 1.0 so as to make no difference for most back of the envelope questions. Strong acids are known to have densities greater than one[5], but that’s not really that useful most of the time.

The Earth has a density of on the order of five. Interestingly, while reading this, I learned that granite and quartz have a density of about three, much less than I had been assuming. No wonder pumice can float.

Gold has a density of about 20 (19 and change, when that matters). Osmium and Iridium are the densest, at around 22 and change.

On the list of interesting curiosities, Saturn is the only planet in the solar system known to have a density less than one, about 0.7! This was only useful in winning a scientific trivia contest with TJFN when I was young.

Scientific Constants:

Avogadro’s number is 6e23, Coulomb’s constant is 9e9, the ideal gas constant is 8.314 (I remember that one because it includes pi), G is 6.67e-11, the Planck constant is 6.63e-34. Most of these are useless without things like the mass or charge of an electron or proton. The only one I use is Avogadro’s number, and that’s largely to calculate how much of your body is made up of atoms which were once part of a particular famous person[7].

For atoms, what I’ve found useful is the fact that a proton is about 2000 times heavier than an electron, and that chemical bond distances are measured in Angstroms (1e-10m).

c is 3e8m/s, which is useful for Star Trek and Star Wars-type arguments. One atmosphere is 101.325kPa, or about 30 feet of water (which is important for divers).

Math constants:

Pi is 3.14159, or 22/7[6] to its friends. Pi comes up a lot.

e is about 2.718. e doesn’t come up very often.

log10(1) = 0
log10(2) ~= 0.301
log10(3) ~= 0.477
log10(7) ~= 0.845
log10(10) = 1

With these three, you can calculate all of the logarithms from one to ten, and much of everything else. In high school, we memorized all of the perfect squares up to 100^2, but most of those have fled from memory.

The (x+y)(x-y) = x^2 – y^2 trick still comes in handy, though.

Large Things:

The CN Tower is 553m tall, really only useful in Toronto.

The Earth has a radius of about 6380m, has an orbit of 93e6 miles (150e6km), useful for things like Dyson Sphere and Red Giant arguments.

The Earth is about 6e24kg, has a diameter of about 40,000km (at the equator), axial tilt of about 23.5 degrees (Uranus is the only planet with an axial tilt significantly greater, almost sideways!).

The sun is about 400x larger than the moon, and is about 400x further away, and this is why solar eclipses work.

Conversions:

1.609 km/mi (0.621 mi/km), 2.54 cm/in (by law!), 9/5+32 degrees C-> degrees F.

SGD, AUD, CAD, USD, EUR, GBP are pretty close in value, and are in that approximate order with only a factor of about 2 separating them. HKD has maybe 6-8 times per unit, CNY is in that general ballpark, and JPY has about 100 times per unit.

Miscellany:

My handspan is about 10″, which is very useful for measuring things.

Stories are about 2m tall.

3600s/hour, 86400 seconds per day, the Unix epoch started 1970-01-01, useful if you spend any time coding, or want to know how long something will take at ‘x per second’. (100k seconds per day is a useful gross approximation for many applications.)

And I would be remiss if I left out my favourite physics approximation (from the same class where I learned about Stirling’s approximation):

sqrt(10) ~= pi.

Thank you and good night.

[1]Although, compare some cases where they are considered not quite so bad practice.

[2]They are also almost essential for proper answering of ‘Fermi Questions‘.

[3]’Tonne’ means metric tonne, or 1000 kg. You can tell because it’s spelled in the French way, and SI (Systeme Internationale) was brought in while France was a preeminent country.

[4]I didn’t know what the actual structure of ice was before looking it up. Apparently, it’s tessellating hexagonal rings.

[5]’Add acid to water, like you oughta’, else you may melt the top of your beaker off.

[6]Really, it isn’t, but it’s a useful approximation sometimes.

[7]With some reasonable approximations, I remember it being billions of atoms with each breath.

The Internet of Thins

March 27, 2016Engineering, Idle Speculation, Internet Culture, Puns, Science!, Thoughts on Thoughts, Words!admin

S and I were walking down the street today, and were thinking about the Internet of Things. Now, it’s a buzzword, and should be taken with a similar-sized grain of salt to all other similar buzzwords.

So we attempted to come up with the worst ideas possible for an Internet of Things.

The first idea was to put chips/sensors in each block in the sidewalk. But thinking about it, that would be really useful. Similar to rail lines[1], there is a widely distributed infrastructure, and checking each part individually is expensive.

Then we thought of putting individual chips/sensors in each tile in a person’s house. How silly would that be? But then you could know exactly what the person was doing, turn lights on and off correctly, rather than the current primitive motion sensors, help people track a daily routine, all kinds of things.

But the last idea we came up with led to the title of this post. What if every cracker you ate had a sensor/chip in it? You would have an almost continuous stream of data about your digestive system, what you were eating, how your body was responding to it. Think of the advances in nutrition science!

And we would owe it all to the Internet of Thins[2].

[1]Look it up! Think about the maintenance costs of surveying 140,000 miles of track.

[2]Gluten-free Wheat Thins for some.

Sufficiently Complex Systems

March 26, 2016Analysis, Engineering, Organizing Systems, Science!, Software Developmentadmin

“Any sufficiently complex computer system is indistinguishable from a biological system.” -Me

So, I like to joke that I find all computer languages equally difficult[1]. The interesting corollary to this is that this also seems to apply to complex systems in general. I approach a complex computer (or other) systems in the same way that I would approach a biological system:

1) Look at the visible behaviour/symptoms/phenotype of the system[2]
2) Assume that there are some number of internal processes in the system, each doing the job they ‘think’ is correct
3) Build a mental model which describes the visible behaviour
4) If debugging a problem, this should greatly narrow down where you investigate

Steps 2) and 3) above are where I think my school training (engineering and science) were the most useful. Our engineering program seemed to focus on the fundamentals and underlying systems, so that one would have a pretty good idea of what individual system components are capable of[3] (and some idea of what the system as a whole is capable of).

The systems I understood most intuitively[4] were chemical systems, probably because my dad and his dad were both chemical engineers. You have a huge number of molecules[5], each doing its own thing, and in aggregate, they exhibit complex behaviour. When you’re dealing with inorganic compounds, you can (most of the time), simulate them in bulk, but when you’re dealing with organic compounds, the complexity explodes and all kinds of strange boundary effects become important.

At this point, you need to switch abstraction levels, also something I remember from engineering, from the micro- level to a level of slightly or substantially more abstraction. At this point, having an intuition about biological systems becomes much more useful.

I’ll use an example to illustrate. At one point, a number of years ago, I and my team were trying to debug why throughput on a system seemed to be capped at a number below the theoretical maximum. Like any flow system, there must be a number of sequential steps that your data or fluid or what have you must flow through. After we built this mental model, it was a matter of looking at readouts and logs to find the graph that had an asymptotic curve showing at which step the system was maxing out. Then we had to fix it, but that’s another story.

[1]This is probably not strictly true. I remember finding Fortran 77 more difficult than usual, and Javascript mind-bendy.

[2]I use ‘behaviour/symptoms/phenotype’, because we might be debugging a problem, or we could just be trying to better understand the system.

[3]This could be why so much of technological advancement is characterized by the advancement in materials. You can only get so far by using a specific set of building blocks. At some point, you need better blocks.

[4]There is a larger article here about how it’s important to follow the things that love the most, whether this is in hobby form or if you’re lucky, work form. You will work harder at doing them better, more importantly, working harder at understanding yourself and removing your mental blocks, which will help you in all the other parts of your life.

[5]Huge.

Nice and Egregious: Shifted Meanings

March 8, 2016Administrivia, Engineering, Nostalgia, Punsadmin

Recently C pointed me to a blog post about the etymology of the word ‘Egregious’. This is especially relevant to me, as you may guess, because of the title I chose for this blog: ‘Sometimes Egregious, Always Gregarious’.

At the time I chose the title, I thought that ‘egregious’ and ‘gregarious’ were almost anagrams of each other, and were only one letter apart. Hence the ‘one letter can make a word of difference'[1]. It turns out that you need to replace the ‘e’ in ‘egregious’ with the ‘ar’ in ‘gregarious’, but I think it’s still apropos and funny.

Anyways, etymology. I also chose the words ‘egregious’ and ‘gregarious’ because I feel they describe me. ‘Egregious’ because I’m often pushing the boundaries[2], or going the ‘third mile'[3]. ‘Gregarious’ because I like talking to people, saying random things when I walk up to strangers. (Come to think of it, ‘Garrulous’ might be better in some situations, but it doesn’t anagram quite as well. Also, it implies a talking requirement that I don’t always fulfill.)

So, now you know more than you thought you needed to about how this blog came to have its title. I hope you’re happy[4].

[1]The phrase ‘One letter can make a word of difference’ came from P, from his rotating .sig file during undergrad. It was routinely a source of wonder for me.

[2]’Pushing the boundaries’ was the motto for my undergrad program, Engineering Science. I enjoy doing this in many ways, the most socially acceptable probably being attempting to solve problems with stupid and outlandish suggestions.

[3]My grandfather was part of the 3T5 class, which decided to give back to the community by instituting a ‘Second Mile’ award. The ‘First Mile’ is the things you normally do, working at work and the things you do at home. The ‘Second Mile’ is ‘going the extra mile’ in service to the community. Our class decided to have an ad hoc ‘Third Mile’ award, which is awarded when ‘You’ve gone too far’.

[4]Really, I do. 😀

alt.comp.risks and Swiss Cheese

January 16, 2016Analysis, Engineering, Nostalgia, Teaching, Thoughts on Thoughtsadmin

If you’ve never read alt.comp.risks, you should do so. In fact, you can read the digest here:

https://catless.ncl.ac.uk/Risks/

If you don’t know what alt.comp.risks is, it is 30 years of all the things that can go wrong with complex systems (especially computers). Anyone who has done a post-mortem or incident report or accident report will familiar (if not happy) reading there. They will probably also notice that the same problems keep happening again and again and again.

Young Drivers mentioned a study* which said that a typical traffic accident requires four errors on the part of the drivers (two each). In the accident and risk analysis world, this is often referred to as the ‘Swiss Cheese’ model. https://en.wikipedia.org/wiki/Swiss_cheese_model

The ‘Swiss Cheese’ model is the idea that adding more layers of checks and protection can help make a system safer, as long as the holes in those layers do not align.

This is a major reason why it is just as important to investigate incidents as it is to investigate accidents. ‘Incidents’ are occasions where something ‘almost went terribly wrong’, where two or more of the ‘Swiss Cheese’ holes aligned, ‘Accidents’ are where all of the ‘Swiss Cheese’ holes aligned, and something terrible actually happened. In the Diagram below**, the ‘Accident’ is the arrow that made it all the way through, all of the other arrows are incidents, which left unchecked, could lead to accidents some day.

Why do we not just spend our time and energy closing those holes in the ‘Swiss Cheese’ (or to making sure they don’t align)? All of that takes money or other resources***. So, given the modern legal system, most organizations balance money and safety in some way, shape, or form. This balance between resource allocation and safety is such an issue that there is an entire regulated profession whose purpose is to properly maintain the balance.

I’m speaking of course of Engineering. The perception of Engineering is perhaps of people building things, or Leah Brahms and Geordi arguing about how to make warp engines go faster, but fundamentally Engineering is about balancing safety with costs.

Probably the most pernicious obstacle to this proper balancing is the dismissal of incidents as unimportant or contained. Any incident which makes its way through 3 of your 4 layers of safety is one mistake away from a disaster, and should be treated accordingly.

*I can’t seem to find it at the moment, but I believe them, as it is consistent with my experience.

**From http://raeda.com.au/?p=115 “The ICAM (Incident Cause Analysis Method) Model Explained

***Often not stated is that spending time on safety-related things is a distraction, both in time and context switching.

“So, what was the issue?”

April 5, 2015Engineering, Software Development, Thoughts on Thoughtsadmin

So, we were debugging a common ground issue today at a in the amazing Helios Makerspace in Montreal.

We got as far as we could ourselves (debugging one common ground problem, and tracking the data signal through one board and on to the second), then we got stuck. We tried a bunch of things, but it was only when the came in, and determine it was two problems: A second common ground problem, combined with the first (Arduino) board having too many outputs and so not outputting a high enough voltage.

The really interesting part (aside from learning again how important common grounds are) was watching the engineers in the room (the people who were building things, perhaps or perhaps not engineers) all run over as soon as the problem was solved and someone asked the question “So, what was the issue?”

Anytime someone is agonizing over a problem for hours, there is bound to be some learning for those around…Thinking about this from a min/maxing perspective, someone spends hours solving the problem, then you spend 2mins learning about the solution, and then you add it to your list of things to try/check when debugging, taking maybe 30s to possibly reduce your own debugging time by hours.