Category Archives: Teaching

On the Importance of Encouraging People to ask (Sincere) Questions

Internet Culture, Teaching, Thoughts on Thoughts, Uncategorized

Recently, a couple of friends of mine shared the following meme:

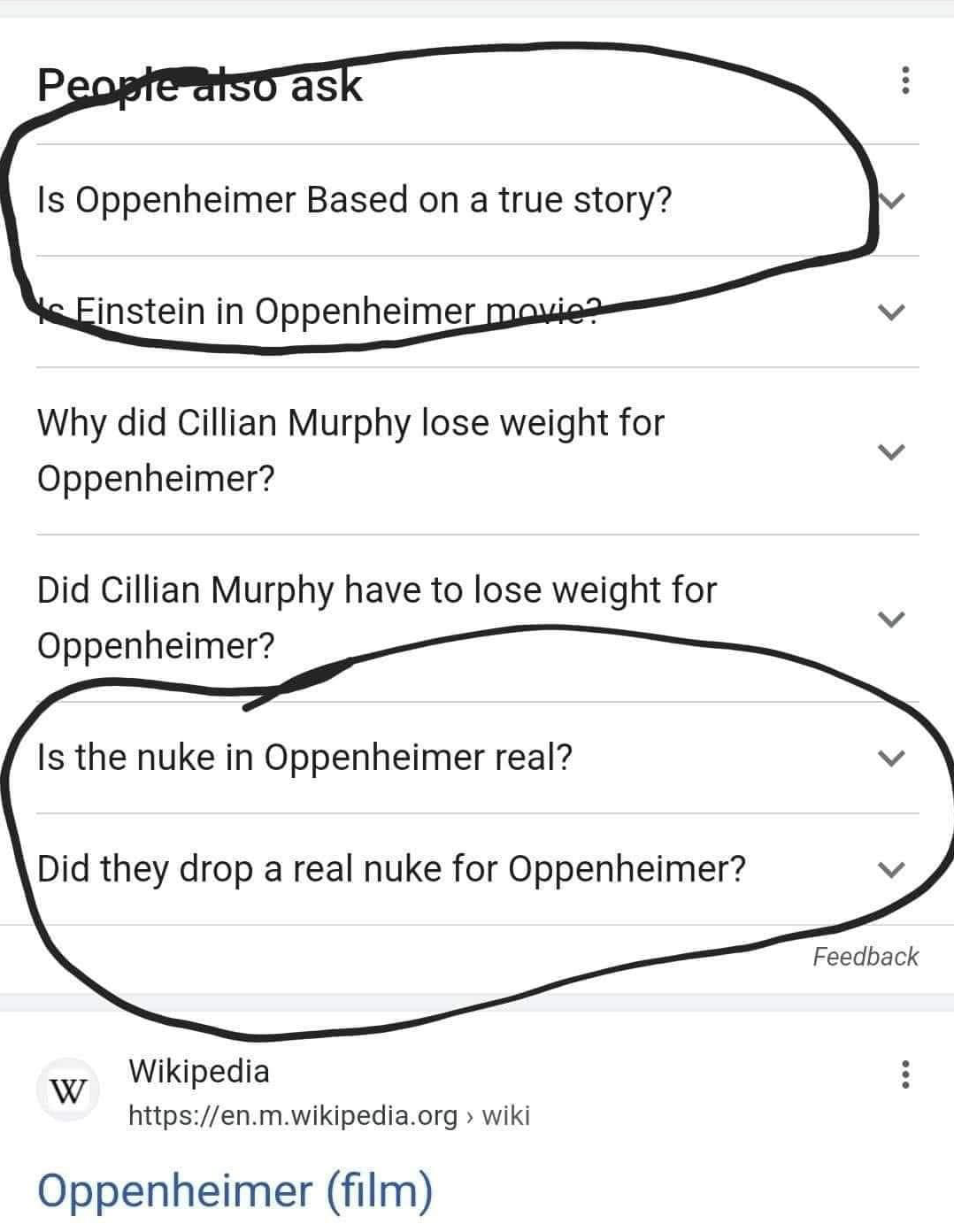
Image of text showing a list of 'People also ask' suggestions from a Google search answering a question about the movie 'Oppenheimer'.
Google Search ‘People also ask’:
(circled) ‘Is Oppenheimer based on a true story’
‘Is Einstein in Oppenheimer movie?
Why did Cillian Murphy lose weight for Oppenheimer?’
‘Did Cillian Murphy have to lose weight for Oppeneimer?’
(circled) ‘Is the nuke in Openheimer real?’
(circled) ‘Did they drop a real nuke for Oppenheimer?’

On the face of it, it may seem harmless, poking some fun at people who not only know less than you, but who know less than you consider reasonable (or perhaps even ‘possible’!)[1].

However, this laughing at others can lead to contempt, and a reluctance in the willingness of others to ask questions, due to the loss of psychological safety.

So, why might people laugh at those who know less about a topic than they?

Some describe surprise as a necessary component of laughter. You can be surprised that others know not just less than you know, but even less than you think is possible to know. This cognitive bias causing this surprise is a subset of the ‘Curse of Knowledge‘, perhaps best summed up by this drawing from Rajesh Mathur:

Curse of Knowledge Bias diagram from Rajesh Mathur: Outer Circle titled 'What you know' Smaller circle titled 'What you expect them to know' Smallest circle titled 'What your audience knows'
Curse of Knowledge Bias diagram from Rajesh Mathur:
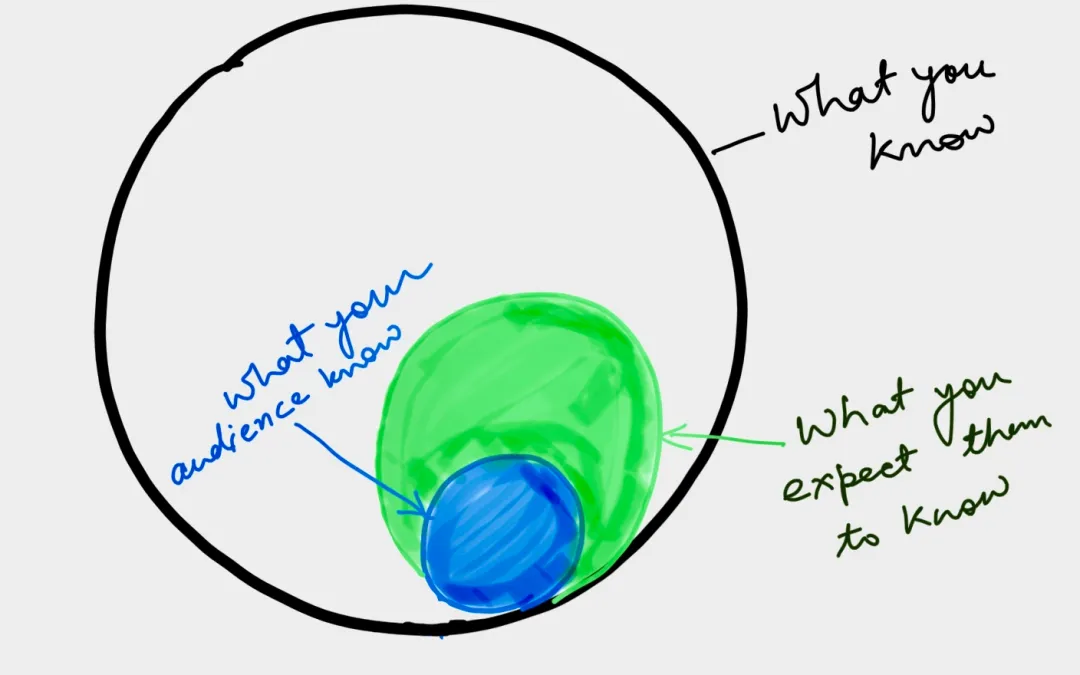
Outer Circle titled ‘What you know’
Smaller circle titled ‘What you expect them to know’
Smallest circle titled ‘What your audience knows’

Sometimes, however, the laughter is not just about surprise, but also comes from a place of insecurity, the desire (conscious or not) to place one’s self above others. This could also be a trauma response, perhaps to experiences with ‘Sealioning‘, where people will repeatedly throw bad-faith questions into a debate or forum instead of engaging with the argument directly.

Another variant of this occurs often in teachers (and oddly enough, IT professionals), where if you’re continually hearing the same question from many different people, it can feel like ‘they just don’t learn'[2], because each year (or semester or day), you get a new person who hasn’t asked that question yet.

So, why might people be asking questions like this?
– They genuinely don’t know: As shown in the diagram above, the variability in knowledge between humans is vast. Even though you know about Oppenheimer because you’ve read multiple books on the subject[3], others might only have a passing knowledge, or even none, despite his pivotal involvement with the start of the Atomic Age.

– They might be mostly sure, but their experience with the thing made them doubt, or they heard a rumor….and the consequence[4] of their assumption being wrong is so large, the ‘importance x likelihood'[5] equation pushes them to ask the question, humans being loss-averse.

– They’re asking a slightly different question: ‘Is Oppenheimer based on a true story’ could mean a lot of different things. There’s a wide range between how much the movie ‘300‘[6] is based on a true story and how much ‘Oppenheimer‘ is. The question could easily be a rephrasing of “how close is the movie ‘Oppenheimer’ to a ‘true story’?”

– They may have difficulties expressing the specific question they want answered: I think it’s worth mentioning that the ability to ask specific targeted questions into a search engine is a (mostly learned) skill, and like all skills, is subject to privilege and ableist gatekeeping. In fact, one could argue that a large part of the uptake of GPT-like software is their ability to answer peoples’ questions when they are not phrased precisely, helping those who are less able to quickly articulate precise thoughts in written form.
– The search engine could be condensing or de-duplicating the wording of questions asked: On a purely technical note, the search engine has a limited amount of space on the page, and it would make sense that they would condense similar questions into perhaps the simplest and clearest version, making it look like people were very commonly asking a simple question.

Thanks for joining me on this wandering journey. I want to learn (and help others learn) to treat others with more kindness, and it’s important to me to deconstruct all of the reasons behind why I (or others) might be doing this. Thanks for reading!

[1] Having done a bunch of teaching, I was aware of the importance of teaching to different styles of learning, and also to different levels of knowledge, but I remember first hearing about this specific subset of this bias relatively recently, probably in a meme, where an expert in a field says ‘how can they not know about this ?’

[2] See also ‘Endless September‘.

[3] Most of my knowledge and understanding of Oppenheimer is from Feynman.

[4] This consequence can be social, such as ‘why didn’t you know about this?’, or personal, such as ‘I don’t want to change the way I think about this unless I have to’, amongst others.

[5] Humans are generally bad at judging the overall expected value of ‘Low-Probability, High-Impact’ events, which is probably why insurance is a thing, although the reduction in distraction/open-loops is probably worth it.

[6] Yes, I know ‘300’ is based on a graphic novel, that’s part of the point I’m trying to make. I’m specifically mentioning 300 because of the large number of known historical inaccuracies and general problematic-ness. There’s also a huge conversation about ‘The Western Canon’ that is out of scope.

The Oft-Hidden Fringe Benefit of a Liberal Arts Education

Idle Speculation, Teaching, Thoughts on Thoughts

“In retrospect, it was so cheap. Only 30,000 a year for people to care about your opinion on art history!”

http://www.smbc-comics.com/comic/final-exam-dram

How does it affect the world to have people in school be told that their (often wrong and terrible) opinions matter? That someone actually cares about their ideas? How does this affect issues of privilege?

Even before grade inflation and students’ expectation of full feedback, students would perform work, someone from the establishment (TA or prof.) would peruse the work, and assign some sort of grade, sometimes with suggestions on how to improve.

But this is not generally true outside of undergrad classes. Questions are not so well defined, answers are often illusory, and generally many fewer people immediately care about the quality of one’s work.

Learning to accept these, I feel, is an important part of growing up. Teaching classes where things are not so well defined is inherently more difficult, and is generally reserved for extremely small class sizes. Illusory answers, or avoiding the ‘easy answer’ can also be difficult for many, as it requires significant introspection. This introspection can also be directed more easily in extremely small class sizes. One also needs to internalize the importance of the quality of one’s work, which is more difficult when someone in power is watching every assignment/essay/exam that one writes.

“No, it was a fantasy. All of those people cared about the quality of my work. Everything mattered so much.”

Perhaps marking of exams and essays persuades people to focus on the minutiae[1], rather than striking out[2] and saying something truly novel and interesting in the ‘real world’ that people actually care about. But maybe it’s important to have small, provable ideas.

But back to the original question. Is it a good or a bad thing to pay money for someone to care about your opinions on art history?

Those with more money can effectively pay to be seen as more important, those with less are forced into other disciplines, or more precarious positions.

At the same time, those in positions of less privilege may find it beneficial to have anyone at all in a position of power care about their writings[3].

“Everything mattered so much.”

When everything matters so much, it can disguise what is actually important[4], but it can also help find new important new things not discoverable by normal methods[5].

Thoughts? Comment below!

[1]I’m not going to address how formal education enhances conformity, that’s a well-known first-order effect.

[2]In this context, ‘striking out’ is an amusing auto-antonym.

[3]Although it can probably be even more devastating if those people in positions of power say that their writings are bad or unimportant.

[4]Analogy: Human civilization changing which traits are passed down.

[5]Analogy: Simulated Annealing.

How do You Think Before You Speak?

Engineering, Idle Speculation, Internet Culture, Politics, Puns, Teaching, Thoughts on Thoughts

I’ve talked a lot about the speed involved and possibly required for retorts and humour, but not all conversation is retorts and counter-retorts[1].

For example, you’re giving a speech or lesson, and someone asks you a question. Many of the same tactics are helpful. It’s helpful to know your audience, to have an idea of their background(s), which types of words will work best for explaining things, and to have an idea of what they perceive the relative level of hierarchy is between you and them.

But once you have an idea of these things, what do you do?

This trigger for this post was an article reporting on Jon Stewart talking about how Hillary Clinton pauses for a few seconds between a question and when she answers[2]:

”
…“It’s — look, there are politicians who are either rendering their inauthenticity in real enough time to appear authentic, and then their are politicians who render their inauthenticity through — it’s like, when your computer … if you have a Mac and you want to play a Microsoft game on it …”

AXELROD: Yes, yes.

STEWART: … and there’s that weird lag.

AXELROD: Yes. No, I mean …

STEWART: That’s Hillary Clinton.

AXELROD: … that’s a big problem. There’s like a seven-second delay and all the words come out in a perfectly …

STEWART: Right.

AXELROD: … politically calibrated sentence.

STEWART: Right. Now, what gives me hope in that is that there’s a delay, which means she’s somehow fighting something. I’ve seen politicians who don’t have that delay and render their inauthenticity in real time, and that’s when you go, ‘That’s a sociopath.’
”

So, when you’re answering a difficult question, do you pause? Why? For how long?

For me, it depends on the type of question. For emotionally difficult questions, some of it is finding a neutral[3] perspective from which to address the question, to speak to the person(s) asking the question in a positive and useful way. Sometimes it’s choosing the appropriate emotional outlet[4] for whatever I’m feeling at the time.

For technically difficult questions, it feels much more like assembling a mental model in my head, or choosing between different visualizations/places to start. Parts of this can feel similar to emotionally difficult questions (perspectives vs. visualizations), but to me they feel quite different[5].

So, how does this work for you?

[1]No matter how much bash.org would want you to think so. (Note that outside that page, bash.org is quite unfiltered internet. You have been warned.)

[2] Article is here. In a footnote because the editorializing in the article is outside the scope of this post.

[3]In the emotional perspective sense.

[4]This is often laughter for later when I’m alone. I mean, really, we’re just ape-like creatures who don’t know the first thing about ourselves. Why are we getting all angry about minutiae? This can only be funny.

[5]Now that I say this, I’ll have to watch next time. But something getting my back[6] up really feels different from trying to focus and assemble a visualization. Maybe being able to relax for all types of questions would make them more similar.

[6]Back hackles?

Slide Rule Accuracy and F=ma

Engineering, Nostalgia, Teaching

Earlier this week, we were talking about drawing a Large diagram as one of the lasting and important things I learned in Prof. Collins’ Structure & Materials course.

Here are some of the others:

‘Slide Rule Accuracy’

This is the idea that in the real world[1], you’re never going to use more than three digits of accuracy (or four if your number starts with a ‘1’)[2]. Beyond that, things will get lost in the noise, or other inaccuracies, whether it’s budget contingencies, manufacturing defects, or whatever. (It would be interesting to see whether this has changed for manufactured parts with increased automation.)

The ‘3 laws of engineering'[3]:

1) F=ma

Simple, yet profound. When you’re dealing with non-relativistic systems (pretty much all of them), you push on something, it will move or react proportionally. This is not limited to physical systems.

2) You can’t push on a rope.

Also simple, has a number of applications for mechanical systems, but is probably the most ‘Engineer-y’ useful statement for dealing with other people.

3) In order to solve an engineering problem, you must first know the solution.

This one doesn’t really make sense on first blush, but I’ve experienced it. I mentioned earlier that the brain is often a structure that problems flow through, and in a sense this is a statement of that. You’re going to try to fit a new problem you’re looking at into the structure(s) of all the problems that you’ve seen before, and you have a huge advantage if you’ve seen similar problems before, or seen other problems you can apply by analogy.

We also had a ‘notebook’ that we put all of our class notes in, including cut and pasting from technical sheets, and this ‘notebook’ was our open book for the exam. It was a great exercise in focusing note-taking and coalescing your thoughts onto a medium-small piece of paper.

“When someone is paying you $100 for an hour of work, it’s worth paying a few extra cents for a good sheet of paper to give it to them on.”

The course had special ‘engineering notepaper’ that they wanted us to hand problem sets in on. There wasn’t any penalty for not doing so, but the lesson was that a little bit of professional presentation went a long way.

[1]This is when you’re dealing with things of reasonable size. I’m guessing when you’re looking at gravity waves or Higgs bosons, you might be using somewhat more accuracy. But at the same time, you’re probably not really looking at more than the last few digits…

[2]This is one of those subtle things which is actually quite important and powerful. On a slide rule, the portion which starts with a ‘1’ is fully 30% of the length (log10(2) ~=0.301), so unless you use the fourth digit here, you’re losing a substantial portion of your accuracy. There is a better explanation of this here:

[3]For a slightly different set of three Engineering laws, look here:

Draw a LARGE Diagram

Engineering, Nostalgia, Organizing Systems, Teaching, Thoughts on Thoughts, Visualizations

Draw a LARGE diagram. When you start, you have no idea which part you’ll be focusing on, so draw it large to start.

In undergrad, we had a Structures and Materials course with Prof. Collins. I owe a lot to that class. It was first year, first term, and it was our first experience with ‘real Engineering’ (with a capital ‘E’).

Collins talked about (along with how to build bridges and other structures) a number of things which you would actually use every day, no matter what types of things you were designing or calculating or planning.

The biggest[1] one is indubitably ‘draw a Large diagram’. Every time I do this, whether it’s on a whiteboard at work, or in my journal[2] at home, it helps far more often than I expect, especially when you’re drawing a teaching diagram, and people are asking questions.

It helps when you’re drawing a semicircle intersected by many lines, with some angles known, some angles not known, and you need to do a bunch of fancy figuring to get the answer[3].

Next time, we’ll talk about some other useful tidbits I learned in that class. Stay tuned!

[1]Ha!

[2]I use notebooks with blank pages. It helps me draw diagrams without extraneous lines, feels freer for thinking.

[3]I think this was a GRE question.

Running A Sprint Planning Meeting

Agile, Idle Speculation, Internet Culture, Nostalgia, Programming, Teaching, Thoughts on Thoughts

It’s the little things that sometimes make a difference. When I was teaching standardized test math so many years ago, I noticed as I was drawing problems on the board, all the little habits that I had picked up. Habits which make solving problems easier, habits which reduce the chance for error.

Things like the curve on the leg of the lower-case ‘t’, so that it doesn’t look like a ‘+’. Curving your ‘x’ so it doesn’t look like a ‘*’ sign.

I think some of this (probably sometimes annoying) attention to detail had carried over to Sprint Planning meetings[1].

Planning Poker is a method for a group to converge on a time estimate for a task or group of tasks. There are a number of ways to do this. The ‘canonical’ way we were taught to do this was to use Fibonacci-numbered cards (1,2,3,,5,Eureka!). This involved a discussion of the task(s) to estimate until everyone had a reasonable idea of their complexity, then each person would choose a number estimate, all of which would be revealed simultaneously, to hopefully reduce bias. The discussion before estimation would not include estimates of how long things were estimated to take, to also try to reduce bias.

While we were running our planning meetings, I noticed that we would start to slip away from this ideal, perhaps because certain things were not important, perhaps because we didn’t see that certain things were important. For example:

We moved from cards to apps, and then to fingers. Using apps for estimation is less annoying than finding the cards each time, but fingers are even faster to find. I/we tried to get around the bias effect by having everyone display their fingers at once, and that worked reasonably well. Even making each person think about their estimate before display can help a lot with reducing the impact of what others might think of them.

One thing I tried which never really caught on when other people were running the meeting was saying ‘A,B,C’ instead of ‘1,2,3’, with the idea that it would be less biasing on the numbers people were choosing. (This may have mostly been an impression of mine, as the moving of the estimate from a mental number to a number of fingers may cement it in a slightly different mental state…)

If one is not careful, and perhaps somewhat impatient in meetings[2], one can start suggesting estimates before they are voted on. It can take considerable discipline and practice to not do this.

Another thing I noticed was how difficult JIRA was to use when one is not practiced in it, especially in a room with many people watching. Something that any experienced[3] demo-giver would know like the back of PowerPoint’s hand.

That’s all I have for now. For more minutiae, tune in tomorrow!

[1]For those of you who have not had the pleasure, these are the meetings at the start of an iteration, where the team sits down in a room, estimates a bunch of priority-ranked tasks, and decides (generally by consensus) how many of them they will commit to getting done in the next two weeks. Like all meetings, they can be good or bad, and the meeting chair (I feel) can make a large difference.

[2]I am probably as guilty of this as anyone. I would recommend Randy Pausch’s ‘Time Management‘ for those who feel similarly.

[3]Read: ‘Battle-scarred’

Pink, and Purple, and Princesses, Oh My!

Idle Speculation, Politics, Teaching

This past weekend, I was at a ‘Saturday Night Meatballs'[1] event with some old friends. Amongst other things, I was watching how the children interacted with each other. There were a collection of children of various ages, from a few different families. Seeing them interacting with their parents, they were all well-loved, and each of the parents were practicing what I would consider modern parenting, setting down firm, well-defined, sensible rules, and encouraging their children to resolve problems themselves by thinking of solutions and implementing them[2].

At the same time, I saw the children self-segregating by gender, both in behaviour and location. One of the parents, talking about a female child mentioned that before they went to daycare, they were into a variety of non-gender-stereotypical things. Almost immediately afterwards, it was Pink and Purple and Princesses. For me, this was a huge stark reminder of the uphill parents face. One could see that even if all of the parents were giving their all to make a non-gender binary household at home, that a culture could persist in a playground or daycare, passed down from year to year by the children.

You can also see it other children’s behaviours. One of the girls wanted to go play with the boys, but was too afraid to go downstairs to the basement[3]. The group of girls sat downstairs for much of the afternoon/evening while the boys ran around and yelled upstairs. When the girls went up to join them, that lasted for a while, the yelling intensified, then they came down to complain about how they were being treated (which prompted the solution-finding conversations above).

I don’t have good answers, just a few observations. I’m sure this is better than it was decades ago, but there’s still a large amount of genderism that we still have to unpack as a society, and it needs to be unpacked early and unconsciously, for the sake of our children.

[1]It’s a great idea, in the tradition of eating together with family and friends to build community. There’s a great description of the ‘original’ Friday Night Meatballs here.

[2]I particularly liked this tactic. The first question is ‘Can I help you think of more options?’, to help the kids develop the coping and problem solving skills to deal with others.

[3]This could also have been because she was new to the group.

Beautiful AI and Go

Games!, Machine Learning, Programming, Teaching, Thoughts on Thoughts

Something monumental happened today. An artificial Go player defeated one of the top human players three times in a row, to win the best of five match

But I want to go back to game two, where Alpha Go played an inhuman and ‘beautiful’ move 37, a ‘very strange move’.

This is what it must be like to have one of your children, or one of your students surpass what you could ever do. You have given them all you can, and they take that and reform it into something beautiful.

They mentioned that Alpha Go plays the entire board at once, and so is more able to see unusual move possibilities like the one above. Fan Hui mentioned that he’s improved (from ranked 633 to in the 300s) as he plays against Alpha Go.

What else can deep learning teach us? What other amazing, inconceivable things will we learn from this new child which is just beginning to flower?

Rotation and Other Metaphors

Analysis, Idle Speculation, Teaching, Thoughts on Thoughts

Today, I noticed that I seem to write a lot about rotation. It seems to come to be ‘naturally’, or at least from something far back in my past[1].

It feels like it might have originally come from discussions of Chirality, somewhere back in high school. Like the concept of Gm1m2/r^2 migrating to Cq1q2/r^2[2], or basing the Bohr model of the atom on the model of the solar system.

A lot of what I write has to do with how I ‘rotate in’ possible solutions to try to fit them with the problem I’m working on. As far as I know, the brain doesn’t actually work like this. I could see a generalized model of computing developing two sections of nerves, one which displayed a problem, one which displayed possible solutions, each in their firing patterns. I wonder if this happens.

While we’re trying to fit possible solutions to this problem, let’s consider other possible metaphors from the ‘ball and stick’ molecular model[3].

– Hinge rotations, like a pendulum, or the dangling COOH on a long-chain carboxylic acid
– Spring action, like atoms in an N2(g) molecule moving towards and away from each other.
– Triangle and higher order into and out of plane rotations/vibrations/translations

Note that all of these can change based on the conditions:
– Temperature
– Water or non-water nearby
– Salts or other charged ions near or far away
– How hydrophilic or hydrophobic parts of the adjoining environment are
– Van der Waals forces

The blog posts which inspired this one:

BOF VI: The Chemist in me:
Multidimensional Word and Sentence Rotation
Solution Rotation

[1] Perhaps this explains why I was so excited about Dinosaur Rotation!

[2]I was lucky enough to see Douglas Hofstadter speak about ‘Analogies in Physics‘. His best work is probably ‘Godel, Escher, Bach‘, which talks about natural and artificial intelligence, the incompleteness theorem, music, and art.

[3]I owe much or all of my intuition here to my time spent rotating[4] through the Ponder Lab at WashU. They work on one of the few world class molecular modeling software programs, Tinker. When I was there, Tinker worked by modeling molecules as balls & sticks, with various rotational and vibrational modes.

[4]Ha!

How do you math?

Analysis, Idle Speculation, Nostalgia, Teaching, Thoughts on Thoughts

In an earlier post, I was talking about ‘friendly triangles’ as an example of unconscious things that inform my interactions with problems and math. Today, I wanted to talk about some other aspects of solving math problems that I didn’t notice I did until I had to teach mental math*, a number of years a.

I was trying to describe mental math, when I noticed all of the little assumptions I made, all the little tricks that I used to make math and mental math easier and more likely to end up correct**.

Some of these tricks were:
– The curve on the bottom of the lower case ‘t’, so it didn’t look like a ‘+’ sign
– Curved ‘x’, I’m guessing so it doesn’t look like a multiplication symbol (this one is lost to the mists of history for me
– Lining up equals signs
– Being very conscious of only having one equality per line
– Friendly triangles (1,1,sqrt(2), 1,2,sqrt(3), 3,4,5)
– Looking for radii of circles in geometry problems
– Various methods for making sure that I always itemized all of the permutations or combinations***

Once I noticed that I was doing these tricks, it was a matter of figuring out which were useful enough to spend my students’ time on. Many of them would probably be most usefully conveyed by demonstration in passing, like the way a painting instructor would demonstrate brush stroke by example.

Knowing then what I know now, I might have tried to help them come up with rules for each type of situation, but in hindsight, it’s probably best I didn’t****. What I do remember is teaching geometry problems with the advice ‘draw a big picture*****’, and ‘label everything you know or can figure out’, which feels like sound advice for solving all sorts of problems.

To this day, it’s probably why all my notebooks are slightly-larger-than-larger blank sketch pads.

*To adults, as part of standardized testing preparation.

**I remember being one of those school math students who did really well overall, but was constantly doing ‘stupid mistakes’, where I would drop a sign, or reverse something/etc… I think I compensated for this be extra checking and all the little tricks I’ll be talking about above. Or have already talked about above, it you’re reading the footnotes after all of the post.

***I actually learned this

****I don’t actually remember what I told them. I seem to recall it was just a bunch of working through problems.

*****Thanks prof. Collins!